Chi-square distribution

Assessment | Biopsychology | Comparative | Cognitive | Developmental | Language | Individual differences | Personality | Philosophy | Social |
Methods | Statistics | Clinical | Educational | Industrial | Professional items | World psychology |

Statistics: Scientific method · Research methods · Experimental design · Undergraduate statistics courses · Statistical tests · Game theory · Decision theory

---

The title of this article should be chi-square distribution or χ² distribution. The initial letter is capitalized due to technical restrictions.

chi-square

Probability density function
Cumulative distribution function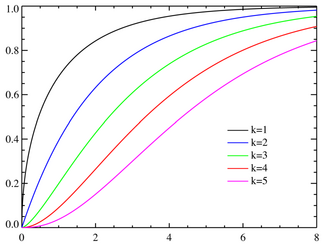
Parameters	$k > 0\,$ degrees of freedom
Support	$x \in [0; +\infty)\,$
pdf	$\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}\,$
cdf	$\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$
Mean	$k\,$
Median	approximately $k-2/3\,$
Mode	$k-2\,$ if $k\geq 2\,$
Variance	$2\,k\,$
Skewness	$\sqrt{8/k}\,$
Kurtosis	$12/k\,$
Entropy	$\frac{k}{2}\!+\!\ln(2\Gamma(k/2))\!+\!(1\!-\!k/2)\psi(k/2)$
mgf	$(1-2\,t)^{-k/2}$ for $2\,t<1\,$
Char. func.	$(1-2\,i\,t)^{-k/2}\,$

In probability theory and statistics, the chi-square distribution (also chi-squared distribution), or χ²  distribution, is one of the theoretical probability distributions most widely used in inferential statistics, i.e. in statistical significance tests. It is useful because, under reasonable assumptions, easily calculated quantities can be proved to have distributions that approximate to the chi-square distribution if the null hypothesis is true.

If $X_i$ are k independent, normally distributed random variables with means $\mu_i$ and variances $\sigma_i^2$, then the statistic

$Z = \sum_{i=1}^k \left(\frac{x_i-\mu_i}{\sigma_i}\right)^2$

is distributed according to the chi-square distribution. This is usually written

$Z\sim\chi^2_k$

The chi-square distribution has one parameter: $k$ - a positive integer which specifies the number of degrees of freedom (i.e. the number of $X_i$)

The chi-square distribution is a special case of the gamma distribution.

The best-known situations in which the chi-square distribution is used are the common chi-square tests for goodness of fit of an observed distribution to a theoretical one, and of the independence of two criteria of classification of qualitative data. However many other statistical tests lead to a use of this distribution, for example Friedman's analysis of variance by ranks.

Properties

The chi-square probability density function is

$f(x;k)= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

where $x \ge 0$ and $f_k(x) = 0$ for $x \le 0$. Here $\Gamma$ denotes the Gamma function. The cumulative distribution function is:

$F(x;k)=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$

where $\gamma(k,z)$ is the incomplete Gamma function.

Tables of this distribution — usually in its cumulative form — are widely available (see the External links below for online versions), and the function is included in many spreadsheets (for example OpenOffice.org calc or Microsoft Excel) and all statistical packages.

If $p$ independent linear homogeneous constraints are imposed on these variables, the distribution of $X$ conditional on these constraints is $\chi^2_{k-p}$, justifying the term "degrees of freedom". The characteristic function of the Chi-square distribution is

$\phi(t;k)=(1-2it)^{-k/2}\,$

The chi-square distribution has numerous applications in inferential statistics, for instance in chi-square tests and in estimating variances. It enters the problem of estimating the mean of a normally distributed population and the problem of estimating the slope of a regression line via its role in Student's t-distribution. It enters all analysis of variance problems via its role in the F-distribution, which is the distribution of the ratio of two independent chi-squared random variables divided by their respective degrees of freedom.

The normal approximation

If $X\sim\chi^2_k$, then as $k$ tends to infinity, the distribution of $X$ tends to normality. However, the tendency is slow (the skewness is $\sqrt{8/k}$ and the kurtosis is $12/k$) and two transformations are commonly considered, each of which approaches normality faster than $X$ itself:

Fisher showed that $\sqrt{2X}$ is approximately normally distributed with mean $\sqrt{2k-1}$ and unit variance.

Wilson and Hilferty showed in 1931 that $\sqrt[3]{X/k}$ is approximately normally distributed with mean $1-2/(9k)$ and variance $2/(9k)$.

The expected value of a random variable having chi-square distribution with $k$ degrees of freedom is $k$ and the variance is $2k$. The median is given approximately by

$k-\frac{2}{3}+\frac{4}{27k}-\frac{8}{729k^2}$

Note that 2 degrees of freedom leads to an exponential distribution.

The information entropy is given by:

$H = \int_{-\infty}^\infty f(x;k)\ln(f(x;k)) dx = \frac{k}{2} + \ln \left( 2 \Gamma \left( \frac{k}{2} \right) \right) + \left(1 - \frac{k}{2}\right) \psi(k/2)$

where $\psi(x)$ is the Digamma function.

Related distributions

• $X \sim \mathrm{Exponential}(\lambda = 2)$ is an exponential distribution if $X \sim \chi_2^2$ (with 2 degrees of freedom).
• $Y \sim \chi_k^2$ is a chi-square distribution if $Y = \sum_{m=1}^k X_m^2$ for $X_i \sim N(0,1)$ independent that are normally distributed. If the $X_i\sim N(\mu_i,1)$ have nonzero means, then $Y = \sum_{m=1}^k X_m^2$ is drawn from a noncentral chi-square distribution.
• $Y \sim \mathrm{F}(\nu_1, \nu_2)$ is an F-distribution if $Y = (X_1 / \nu_1)/(X_2 / \nu_2)$ where $X_1 \sim \chi_{\nu_1}^2$ and $X_2 \sim \chi_{\nu_2}^2$ are independent with their respective degrees of freedom.
• $Y \sim \chi^2(\bar{\nu})$ is a chi-square distribution if $Y = \sum_{m=1}^N X_m$ where $X_m \sim \chi^2(\nu_m)$ are independent and $\bar{\nu} = \sum_{m=1}^N \nu_m$.
• if $X$ is chi-square distributed, then $\sqrt{X}$ is chi distributed.

Various chi and chi-square distributions

Name	Statistic
chi-square distribution	$\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2$
noncentral chi-square distribution	$\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2$
chi distribution	$\sqrt{\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}$
noncentral chi distribution	$\sqrt{\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2}$

See also

• Cochran's theorem
• Inverse-chi-square distribution

External links

• Overview of Chi-Square Test
• On-line calculator for the significance of chi-square, in Richard Lowry's statistical website at Vassar College.
• Distribution Calculator Calculates probabilities and critical values for normal, t-, chi2- and F-distribution

de:Chi-Quadrat-Verteilung es:Distribución chi-cuadrado fr:Loi du χ² nl:Chi-kwadraatverdeling ru:Хи-квадрат распределение su:Sebaran chi-kuadrat fi:Khii toiseen -jakauma sv:Chitvåfördelning zh:卡方分佈